数学，作为自然科学的皇后，一直以来以其独特的魅力吸引着无数探索者，整式规律，作为数学领域的一个重要分支，更是以其深邃的内涵和广泛的应用领域成为了研究的热点，本文将围绕“整式规律专题（2017）”这一主题展开，探讨其研究背景、内容、方法以及应用前景。

整式规律专题的研究背景

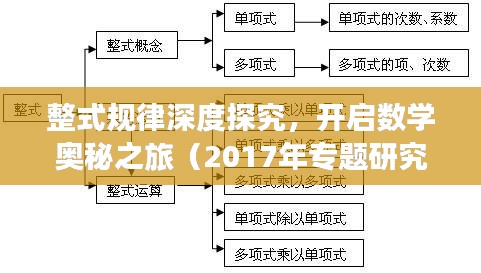
整式是数学中代数式的一种基本形式，它包含单项式和多项式，整式规律研究的是整式中各项之间的关系及其变化规律，随着数学研究的深入，整式规律在代数、几何、数论等领域的应用越来越广泛，其重要性也日益凸显，2017年，整式规律专题的研究进入了一个新的阶段，各种新的理论和方法不断涌现。

在整式规律专题研究中，研究者们主要关注以下几个方面：

1、整式的性质与结构：研究整式的基本性质，如交换律、结合律等，以及整式的结构特点，如对称整式、循环整式等。

2、整式的运算规律：研究整式在运算过程中的变化规律，如加法、减法、乘法、除法等。

3、整式的应用：探讨整式在代数、几何、数论等领域的应用，如求解方程、几何图形的性质等。

整式规律专题的研究方法

在整式规律专题研究中，常用的研究方法包括：

1、归纳法：通过观察和分析具体的例子，总结出一般的规律。

2、演绎法：从已知的规律出发，推导出新的结论。

3、数学软件辅助研究：利用数学软件，进行符号计算、数值计算等，辅助研究整式规律。

2017年整式规律专题的研究进展

在2017年，整式规律专题的研究取得了许多重要的进展，研究者们发现了一些新的整式性质和结构，揭示了整式在运算过程中的新规律，整式在代数、几何等领域的应用也得到了进一步的拓展，特别是在求解复杂方程和几何图形性质方面，整式规律的应用显得尤为重要。

整式规律专题的应用前景

整式规律在数学及其他领域的应用前景广阔，在数学领域，整式规律的研究有助于推动代数、几何、数论等分支的发展，在实际应用中，整式规律可以应用于物理、化学、生物等领域，如量子力学、化学反应速率、生物信息学等，整式规律还可以应用于计算机科学、金融等领域，如算法设计、数据分析等。

本文围绕“整式规律专题（2017）”这一主题，探讨了整式规律的研究背景、内容、方法以及应用前景，整式规律作为数学领域的一个重要分支，其深邃的内涵和广泛的应用领域使得它成为了研究的热点，随着研究的深入，整式规律的应用前景将更加广阔。